Time Value of Money Explained – Part 1

The Time Value of Money states that a dollar today is worth more than a dollar in the future. The reason is straightforward: a dollar today can be invested and start earning interest immediately. Interest is the fee charged for the use of money, expressed as a percentage rate over a specific period.
Therefore, this principle has three major implications for financial decisions:
- Incomparable Cash Flows: Money received at different times cannot be directly compared. For example, receiving $100 today is not equivalent to receiving $100 a year from now.
- The Need for a Common Yardstick: Consequently, to compare cash flows occurring at different times, we must account for the potential earning capacity of money.
- Interest is the Engine: Furthermore, moving money forward or backward in time for comparison requires measuring its interest potential.
Understanding the Future Value Factor
We use the Future Value (FV) Factor, which allows us to calculate the value of a present sum of money at a future time. In other words, it answers the question: “If I invest this much today, how much will it be worth later?”
The formula for the future value of a single sum is:
$$
FV = PV \times (1 + r)^T
$$
Where:
- \(FV\) = Future Value
- \(PV\) = Present Value
- \(r\) = Interest rate per period
- \(T\) = Number of periods
For example, let’s assume you invest $100 in a bank account that pays a 10% annual interest rate. Step by step, here’s what happens
- After 1 year:
$$
FV = 100 \times (1 + 0.10)^1 = 100 \times 1.10 = 110
$$
- After 2 years:
$$
FV = 100 \times (1 + 0.10)^2 = 100 \times 1.21 = 121
$$
As you can see, in each year, interest is earned not only on the original $100 but also on the accumulated interest from previous years. This process is called compounding.
The Future Value Factor \((1 + r)^T \)is what drives this growth, making it possible to compare the value of money across different time periods.
Finally, what happens if the interest rate changes to 5% or 15% and the time horizon extends to 6–10 years? Below are some charts to help you visualize and better understand this effect.
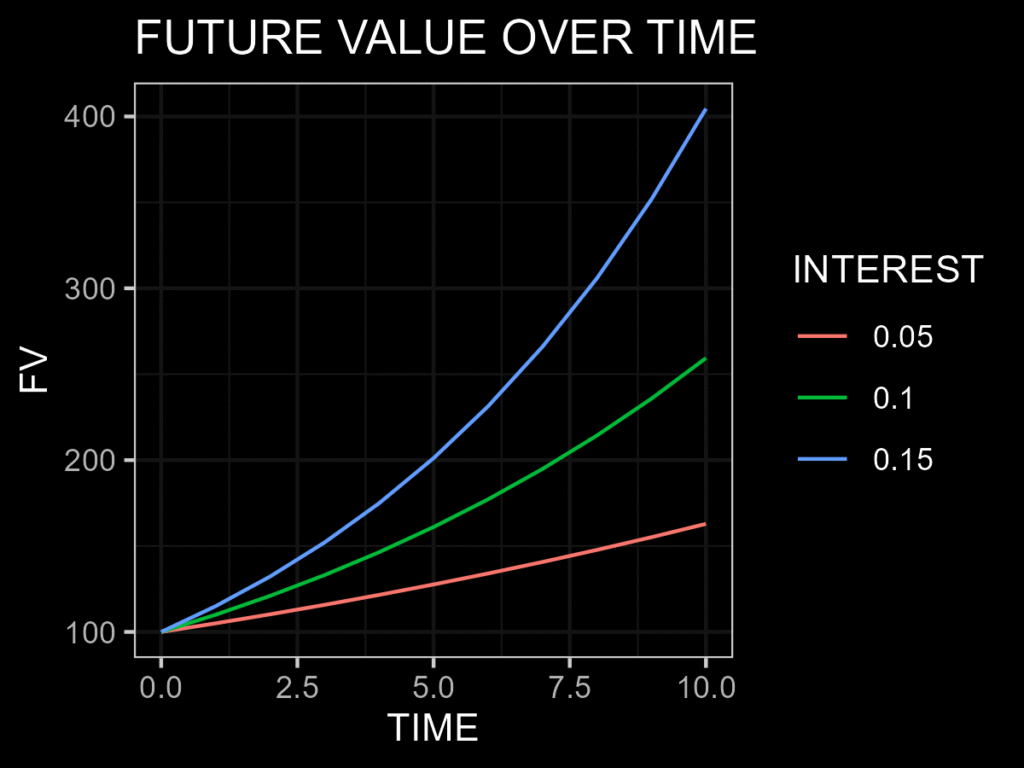
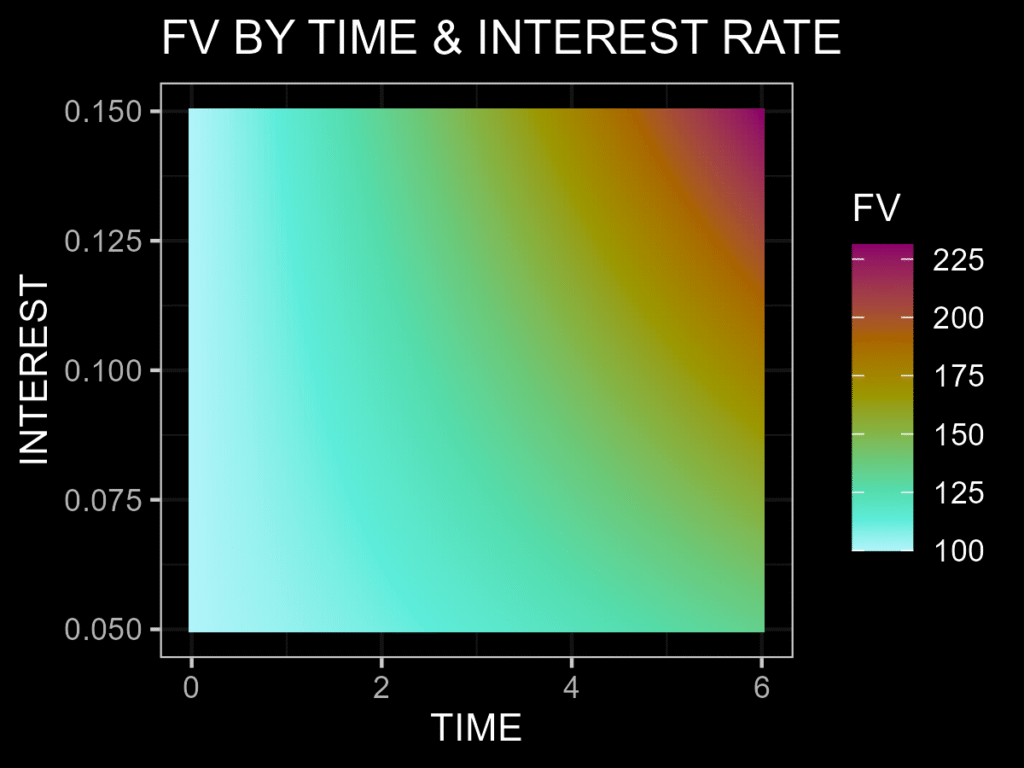
More about time value of the money
Coming Soon..,