Understanding Little’s Law: A Guide to Key Operational Metrics.

Little’s Law: An Introduction
Today we are going to dive into Little’s Law. This is one of the fundamental principles in operations management and queuing theory. It provides a simple but powerful relationship between three key performance measures in any stable system:
Little’s Law can give us answers to questions such as:
- If there are, on average, 50 customers per day in a hotel and each customer stays for an average of 3 days, how many rooms should the hotel have on average?
- During a peak lunch hour at a Subway, if there are, on average, 4 customers in the line and the store serves customers at a rate of 1 per minute, what is the average waiting time for a customer?
The Formula
Doesn’t that sound quite practical? The mathematical formula for the law is very simple and is easy to understand at first, but becomes quite tricky when you think about it more deeply.
The law states:
I=R×T
I (Inventory): The average number of inventory(or items, customers, jobs, tasks, etc.) in the work in process.
R (Throughput Rate): The average rate at which items enter and leave the system.
T (Throughput time): The average time an item spends in the system.
The Stability Condition
Note: The system must be stable, meaning the average input rate equals the average output rate over the long run. For example, when a store serves customers at a rate of 1 per minute and customers arrive at a rate of 2 per minute, the system is not stable because the line increases continuously. In such a scenario, Little’s Law does not apply.
Answer the Questions
Let’s answer the previous questions using Little’s Law.
Hotel Question
The question asks for the number of rooms, which represents the average number of customers in the system, or Inventory (I).
- R (Throughput Rate): 50 customers/day
- T (Throughput Time): 3 days
- I=R×T
- I=(50 customers/day)×(3 days)=150 rooms
So, the hotel should have 150 rooms on average.
Subway Question
The question asks for the average waiting time for a customer, which is the Throughput Time (T). The inventory, I, is the number of customers in the line.
- I (Inventory): 4 customers
- R (Throughput Rate): 1 customer/minute
- T=I/R
- T=(4 customers)/(1 customer/minute)=4 minutes
So, the average waiting time for a customer in the line is 4 minutes.
Deeper Dive into Process Analysis
Now, with the Subway example, let’s connect Little’s Law to the process analysis we have done so far, so that we can clarify process analysis more deeply.
First, let’s assume the Subway has just one employee who has a capacity of 1 order per minute. In this case, how is the inventory (customer’s order, or the customer themselves) placed in this whole process? The process can be represented as the following process mapping.
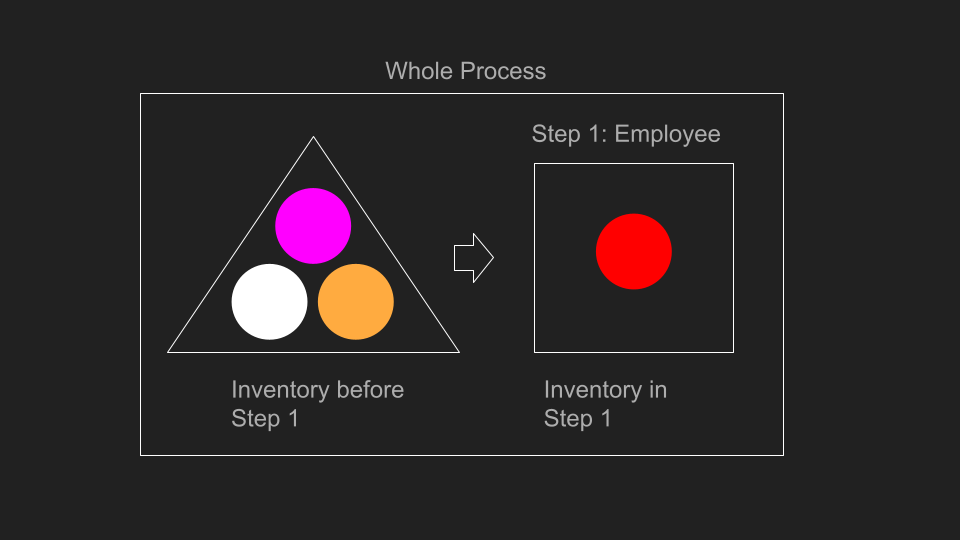
In this diagram, the Whole Process is the entire system,. The Inventory before Step 1 represents the customers in the line, while the Inventory in Step 1 represents the single customer being served.
Run Time vs. Throughput Time
Do you understand why an employee can handle 1 customer per minute, but a customer waits 4 minutes to be handled? To understand this, we need to understand the difference between Run Time and Throughput Time.
Let’s assume there is no setup time for the employee’s process. In this case, the Run Time is the inverse of capacity, which is one minute per customer. This is the pure processing time that an employee takes to complete one customer’s order. This time does not consider waiting time.
However, Throughput Time is a more comprehensive measure. It includes not only the run time, but also any time spent waiting in the queue. This is why a customer’s throughput time is 4 minutes, even though the run time is only 1 minute.
The Impact of Setup Time
If there is a setup time, we need to understand one more thing: Cycle Time. Let’s assume the employee has to shift with another employee, and it takes 12 minutes to do so. This setup time is a one-time cost for the batch of work.
Let’s assume the employee can serve 60 customers.
- Without the setup time, it takes 60 minutes to handle 60 customers (1 minute/customer). The Run Time is 1 minute per customer.
- With the setup time, it takes 72 minutes (60 + 12) to handle 60 customers.
The Cycle Time is the time it takes to produce one unit in a batch, including the setup time. In this case, the cycle time is:
72 minutes/60 customers=1.2 minutes/customer
With this setup time, the capacity is no longer one customer per minute; it is now:
1/1.2=0.833 customers/minute
If there are four customers on average in the line, new throughput time becomes:
T=I/R=4 customers/0.833 customers/minute=4.8 minutes
So the new throughput time becomes 4.8 minutes, which means customers now wait longer.
The Relationship Between Key Terms
Let’s clarify what is meant by “inventory is on average” in Little’s Law. When we say inventory is “on average,” it means that the system is stable, and the average number of items inside is constant over the long run.
This stability is a key assumption for Little’s Law to be valid. The stability of the system is determined by the relationship between the Arrival Rate and the Capacity.
The relationship is:
- If Arrival Rate ≤ Capacity, the system is stable. In this case, the Throughput Rate will be equal to the Arrival Rate. The line will not grow infinitely. Little’s Law applies.
- If Arrival Rate > Capacity, the system is unstable. In this case, the Throughput Rate will be equal to the Capacity. The line will grow infinitely, and Little’s Law does not apply because there is no stable average inventory.
- Capacity is the maximum rate a process can handle. It is an intrinsic property of the system (e.g., how fast the employee works).
- Arrival Rate is the rate at which items (customers) enter the system. This is a characteristic of the environment.
- Throughput Rate (R) is the actual rate at which items are processed. It is always limited by the lesser of the Arrival Rate and the Capacity.
R=min(Arrival Rate,Capacity)