Turning Functions into Vectors and Understanding the Adjoint Operator
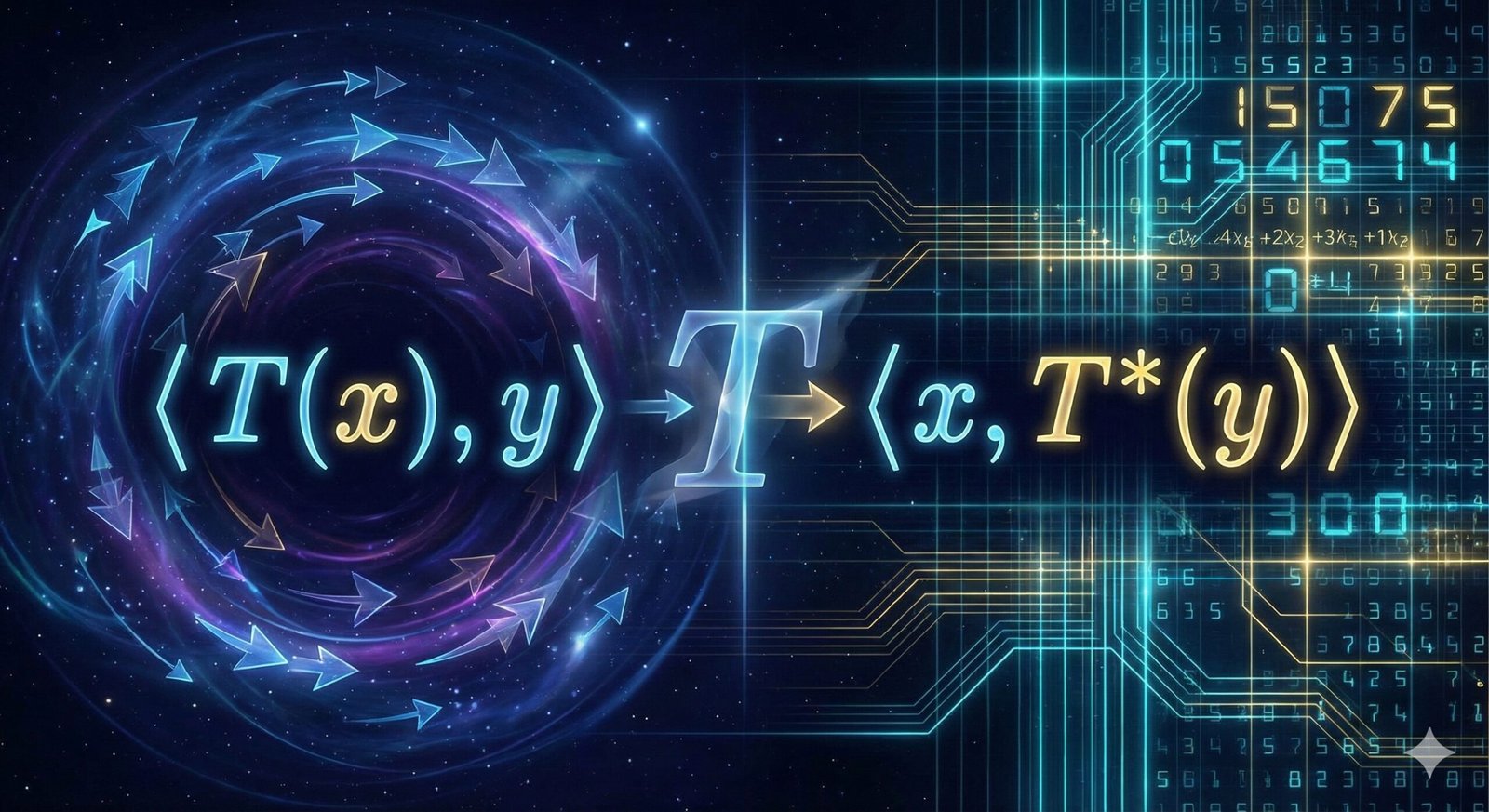
I will start by showing that complex linear “machines” (functions) can essentially be replaced by a single, unique vector. Then, we will learn how to “flip” operators from one side of an inner product to the other, and finally, we will see how this abstract concept translates directly into the “conjugate transpose” of a matrix.
Theorem 6.8
Let \(V\) be a finite-dimensional inner product space over \(F\), and let \(g: V \to F\) be a linear transformation. Then there exists a unique vector \(y \in V\) such that \(g(x) = \langle x, y \rangle\) for all \(x \in V\).
In simple terms, this theorem tells us that any linear function that maps a vector to a scalar can be represented by a simple inner product.
Think of \(g\) as a “machine” that takes a vector and gives you a number. This theorem says you don’t need to understand the complex workings of that machine. Instead, for every such machine, there exists a specific, unique vector \(y\) that does the exact same job using the inner product.
This is powerful because it allows us to treat abstract functions as if they were just vectors.
A Simple Example
Let’s look at the standard 2D space, \(V = \mathbb{R}^2\), where the inner product is the standard inner product (See the previous post on ‘inner product’):
- Define the function: Suppose we have a linear transformation \(g: \mathbb{R}^2 \to \mathbb{R}\) defined by: $$
g(x_1, x_2) = 3x_1 – 5x_2
$$ - Apply the theorem: The theorem guarantees there is a vector \(y = (y_1, y_2)\) such that computing the dot product \(\langle x, y \rangle\) gives the exact same result as \(g(x)\).
- Find the vector: We set them equal: $$
3x_1 – 5x_2 = x_1y_1 + x_2y_2
$$ By comparing the coefficients, it is obvious that \(y_1 = 3\) and \(y_2 = -5\).
Result: The unique vector is \(y = (3, -5)\). The function \(g\) is now completely represented by this single vector.
Theorem 6.9 (The Adjoint Operator \(T^*\))
Let \(V\) be a finite-dimensional inner product space, and let \(T\) be a linear operator on \(V\). Then there exists a unique function \(T^:V \to V\) such that \(\langle T(x), y \rangle = \langle x, T^*(y) \rangle\) for all \(x, y \in V\). Furthermore, \(T^*\) is linear.
This theorem allows us to move a linear operator \(T\) from the left side of an inner product to the right side. When we do this, the operator changes into its adjoint, denoted as \(T^*\).
How can we find the adjoint operator \(T^*\)? The next theorem will give us the answer.
Theorem 6.10: The Matrix of the Adjoint
1. The Theorem Statement
Let \(V\) be a finite-dimensional inner product space, and let \(\beta\) be an orthonormal basis for \(V\). If \(T\) is a linear operator on \(V\), then:
$$
[T^*]_\beta = [T]_\beta^*
$$
This theorem connects the abstract concept of an adjoint operator (\(T^*\)) to the concrete world of matrices. It tells us that if we choose our coordinate system correctly (an orthonormal basis), finding the adjoint is as simple as taking the conjugate transpose of the matrix.
2. A Simple Example in \(\mathbb{C}^2\)
Let’s break this down step-by-step to see exactly where the numbers come from.
The Setup
- Space: We are working in \(V = \mathbb{C}^2\).
- Basis (\(\beta\)): We use the standard ordered basis \({e_1, e_2}\). These are the standard unit vectors: $$
e_1 = \begin{pmatrix} 1 \\ 0 \end{pmatrix}, \quad e_2 = \begin{pmatrix} 0 \\ 1 \end{pmatrix}
$$ Note: This is an orthonormal basis because the length of each vector is 1, and they are perpendicular (their inner product is 0).
The Operator (\(T\))
Let’s define a linear operator \(T\) by how it transforms a vector \(\begin{pmatrix} z_1 \ z_2 \end{pmatrix}\):
$$
T \begin{pmatrix} z_1 \\ z_2 \end{pmatrix} = \begin{pmatrix} z_1 + 5i z_2 \\ 2z_1 + 3z_2 \end{pmatrix}
$$
Step 1: Constructing the Matrix \([T]_\beta\)
To find the matrix representation of \(T\), we apply \(T\) to each basis vector and write the results as the columns of our matrix.
- Apply \(T\) to \(e_1\): $$
T(e_1) = T \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 + 5i(0) \\ 2(1) + 3(0) \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \end{pmatrix}
$$ This becomes the first column. - Apply \(T\) to \(e_2\): $$
T(e_2) = T \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 + 5i(1) \\ 2(0) + 3(1) \end{pmatrix} = \begin{pmatrix} 5i \\ 3 \end{pmatrix}
$$ This becomes the second column.
So, the matrix representation is:
$$
[T]_\beta = \begin{pmatrix} 1 & 5i \\ 2 & 3 \end{pmatrix}
$$
Step 2: Finding \([T^*]_\beta\) using the Theorem
Now we want the matrix for the adjoint operator, \(T^*\). Because our basis \(\beta\) is orthonormal, Theorem 6.10 allows us to simply take the conjugate transpose of the matrix we just found.
- Transpose (swap rows and columns): $$
\begin{pmatrix} 1 & 2 \\ 5i & 3 \end{pmatrix}
$$ - Conjugate (flip the sign of imaginary parts): $$
\begin{pmatrix} 1 & 2 \\ -5i & 3 \end{pmatrix}
$$
Conclusion:
$$
[T^*]_\beta = \begin{pmatrix} 1 & 2 \\ -5i & 3 \end{pmatrix}
$$
Corollary to Theorem 6.10
1. The Corollary Statement
Let \(A\) be an \(n \times n\) matrix. Then:
$$
L_{A^*} = (L_A)^*
$$
2. What does this mean?
This might look like alphabet soup, so let’s decode the symbols:
- \(L_A\) is the “Left Multiplication” operator. It turns a static matrix \(A\) into a function. It simply means “the function that multiplies vectors by \(A\).”
- \(A^*\) is the conjugate transpose of the matrix \(A\) (swap rows/cols and flip signs of \(i\)).
- \((L_A)^*\) is the adjoint operator of the function \(L_A\).
If your linear operator is just “multiplication by matrix \(A\),” then the adjoint of that operator is just “multiplication by the conjugate transpose of \(A\).”
This confirms that for standard vector spaces (\(\mathbb{F}^n\)) with the standard dot product, the abstract definition of an adjoint coincides exactly with the matrix conjugate transpose.
3. A Simple Example
Let’s reuse the matrix \(A\) from our previous example to see this relationship in action.
The Matrix (\(A\)):
$$
A = \begin{pmatrix} 1 & 5i \\ 2 & 3 \end{pmatrix}
$$
The Operator (\(L_A\)):
This is the function defined by \(L_A(x) = Ax\).
$$
L_A \begin{pmatrix} z_1 \\ z_2 \end{pmatrix} = \begin{pmatrix} 1 & 5i \\ 2 & 3 \end{pmatrix} \begin{pmatrix} z_1 \\ z_2 \end{pmatrix}
$$
Applying the Corollary:
We want to find the adjoint operator, \((L_A)^*\).
The corollary says we don’t need to do any integration or abstract algebra. We just find the matrix \(A^*\) and multiply by that.
$$
A^* = \begin{pmatrix} 1 & 2 \\ -5i & 3 \end{pmatrix}
$$
Therefore, the adjoint operator is:
$$
(L_A)^*(x) = L_{A^*}(x) = \begin{pmatrix} 1 & 2 \\ -5i & 3 \end{pmatrix} x
$$
Summary:
The adjoint of “multiply by A” is “multiply by A-conjugate-transpose.”
Theorem 6.11: Properties of the Adjoint
1. The Theorem Statement
Let \(V\) be an inner product space, and let \(T\) and \(U\) be linear operators on \(V\). Then:
(a) \((T + U)^* = T^* + U^*\)
(b) \((cT)^* = \bar{c} T^*\) (for any scalar \(c\))
(c) \((TU)^* = U^* T^*\)
(d) \(T^{**} = T\)
(e) \(I^* = I\)
2. What does this mean?
Most of these properties are intuitive, but two of them ((b) and (c)) are common traps where students make mistakes.
- Property (a) Additivity: The adjoint of a sum is the sum of the adjoints. This is straightforward.
- Property (b) Conjugate Scaling (Watch out!): If you multiply an operator by a scalar \(c\), the adjoint is multiplied by the complex conjugate \(\bar{c}\).
- Example: If you scale \(T\) by \(i\), the adjoint is scaled by \(-i\).
- Property (c) Reverse Order (The “Shoes and Socks” Rule): When you take the adjoint of a product (composition), you must reverse the order of the operators. \((TU)^*\) is \(U^* T^*\), *not* \(T^* U^*\).
- Analogy: Think of this like inverses. If you put on socks (\(T\)) then shoes (\(U\)), to reverse the process you must take off shoes \((U^*)\) first, then socks \((T^*)\).
- Property (d) Involution: Taking the adjoint twice gets you back to where you started. \(T^{**} = T\).
3. A Simple Example (Verifying the “Reverse Order” Rule)
Let’s check Property (c) using matrices in \(\mathbb{C}^2\). We want to verify that \((TU)^* = U^* T^*\).
The Setup
Let’s define two operators using these matrices:
$$
T = \begin{pmatrix} 0 & i \\ 1 & 0 \end{pmatrix}, \quad U = \begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix}
$$
Left Side: \((TU)^*\)
First, multiply \(T\) and \(U\), then take the adjoint.
- Product \(TU\): $$
TU = \begin{pmatrix} 0 & i \\ 1 & 0 \end{pmatrix} \begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix} = \begin{pmatrix} 0 & 3i \\ 2 & 0 \end{pmatrix}
$$ - Adjoint \((TU)^*\): (Transpose and Conjugate) $$
(TU)^* = \begin{pmatrix} 0 & 2 \\ -3i & 0 \end{pmatrix}
$$
Right Side: \(U^* T^*\)
First, find the adjoints individually, then multiply them in reverse order.
- Find Adjoints: $$
T^* = \begin{pmatrix} 0 & 1 \\ -i & 0 \end{pmatrix}, \quad U^* = \begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix}
$$ (Note: \(U\) is real and diagonal, so \(U^ = U\). \(T\) has an \(i\), so the sign flips).* - Product \(U^* T^*\): $$
U^* T^* = \begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix} \begin{pmatrix} 0 & 1 \\ -i & 0 \end{pmatrix} = \begin{pmatrix} 0 & 2 \\ -3i & 0 \end{pmatrix}
$$
Conclusion
Both sides equal \(\begin{pmatrix} 0 & 2 \\ -3i & 0 \end{pmatrix}\). The theorem holds!
Corollary to Theorem 6.11: Matrix Properties
1. The Corollary Statement
Let \(A\) and \(B\) be \(n \times n\) matrices. Then the following properties hold:
(a) \((A + B)^* = A^* + B^*\)
(b) \((cA)^* = \bar{c}A^*\) for all scalars \(c \in F\)
(c) \((AB)^*\) = \(B^*A^*\)
(d) \(A^{**} = A\)
(e) \(I^* = I\)
2. What does this mean?
This corollary confirms that the rules we just learned for abstract linear operators apply exactly the same way to matrices.
Because every \(n \times n\) matrix represents a linear operator (specifically, \(L_A(x) = Ax\)), we can translate the operator theorems directly into matrix arithmetic. This is incredibly useful for computations because you don’t have to worry about the underlying vector space definitions—you can just follow these algebraic rules.
3. A Simple Example (Verifying Scalar Multiplication)
Let’s look at Property (b): \((cA)^* = \bar{c}A^*\). This is a very common place to make a small mistake by forgetting to take the complex conjugate of the scalar.
- The Setup: Let \(c = i\) (the imaginary unit). Let Matrix \(A = \begin{pmatrix} 1 & 2 \\ 0 & i \end{pmatrix}\).
- Left Side: \((cA)^*\) First, multiply \(c\) into the matrix, then take the conjugate transpose.
- \(cA = i \begin{pmatrix} 1 & 2 \\ 0 & i \end{pmatrix} = \begin{pmatrix} i & 2i \\ 0 & -1 \end{pmatrix}\)
- Now, transpose and conjugate: $$
(cA)^* = \begin{pmatrix} -i & 0 \\ -2i & -1 \end{pmatrix}
$$
- Right Side: \(\bar{c}A^*\) First, find the conjugate of \(c\) and the conjugate transpose of \(A\), then multiply.
- \(\bar{c} = -i\).
- \(A^* = \begin{pmatrix} 1 & 0 \\ 2 & -i \end{pmatrix}\) (Transpose \(A\), then flip sign of \(i\)).
- Multiply them: $$
\bar{c}A^* = -i \begin{pmatrix} 1 & 0 \\ 2 & -i \end{pmatrix} = \begin{pmatrix} -i & 0 \\ -2i & (-i)(-i) \end{pmatrix} = \begin{pmatrix} -i & 0 \\ -2i & -1 \end{pmatrix}
$$
Conclusion:
Both sides equal \(\begin{pmatrix} -i & 0 \\ -2i & -1 \end{pmatrix}\). The property holds!
We have now completed the drafts for:
- Theorem 6.10 & Corollary (Matrix of the Adjoint)
- Theorem 6.11 & Corollary (Properties of the Adjoint)
References
The theorem numbering in this post follows *Linear Algebra* (4th Edition) by Friedberg, Insel, and Spence. Some explanations and details here differ from the book.