Functions

Why Use Functions in Business?

Functions are a way to translate real-world situations into mathematical language. But why do we do this? One important reason is to solve real-world problems.

Take a small business as an example. Suppose you’re trying to figure out the best price for your product to maximize profit. You might already have a rough idea based on your experience. However, if you can express the demand curve and cost structure as mathematical functions, you can apply mathematical tools to determine the exact price point that maximizes profits.

When Do We Use Functions?

There are many situations where one variable depends on another. For example, the cost per product (let’s say \(y\) may vary depending on the amount of production (denoted as \(x\). In such cases, we say that cost is a function of quantity—in other words, \(y\) is a function of \(x\). And we write this symbolically as

$$y = f(x)$$

and read “\(y\) equals \(f\) of \(x\)“.

Here, the symbol \(f\) represents the function, \(x\) is the independent variable representing the input value of \(f\), and \(y\) is the dependent variable or output value of \(f\) at \(x\).

All the possible values that \(x\) (the quantity of production) can take are called the domain. In this case, the domain would be \(x \geq 0\), since negative production doesn’t make sense. Similarly, all the possible values that \(y\) (cost) can take are called the range. The range would also be \(y \geq 0\), as cost cannot be negative.

How Can We Define Functions with Formal Symbols?

Now let’s wrap up by learning how to express functions using formal and elegant mathematical notation. Let’s take a moment to appreciate the definition of functions provided by Thomas, a standard in many calculus textbooks.

DEFINITION A function \(f\) from a set \(D\) to a set \(Y\) is a rule that assigns a unique (single) element \(f(x) \in Y\) to each element \(x \in D\).

Here, \(\in\) means “belongs to” or “is an element of.”

Example

Let’s look at an example. Assume the domain \(D = {a, b, c, d}\) and the range \(Y = {E, F, G, H}\). Then one possible function \(f(x)\) can be defined as follows.

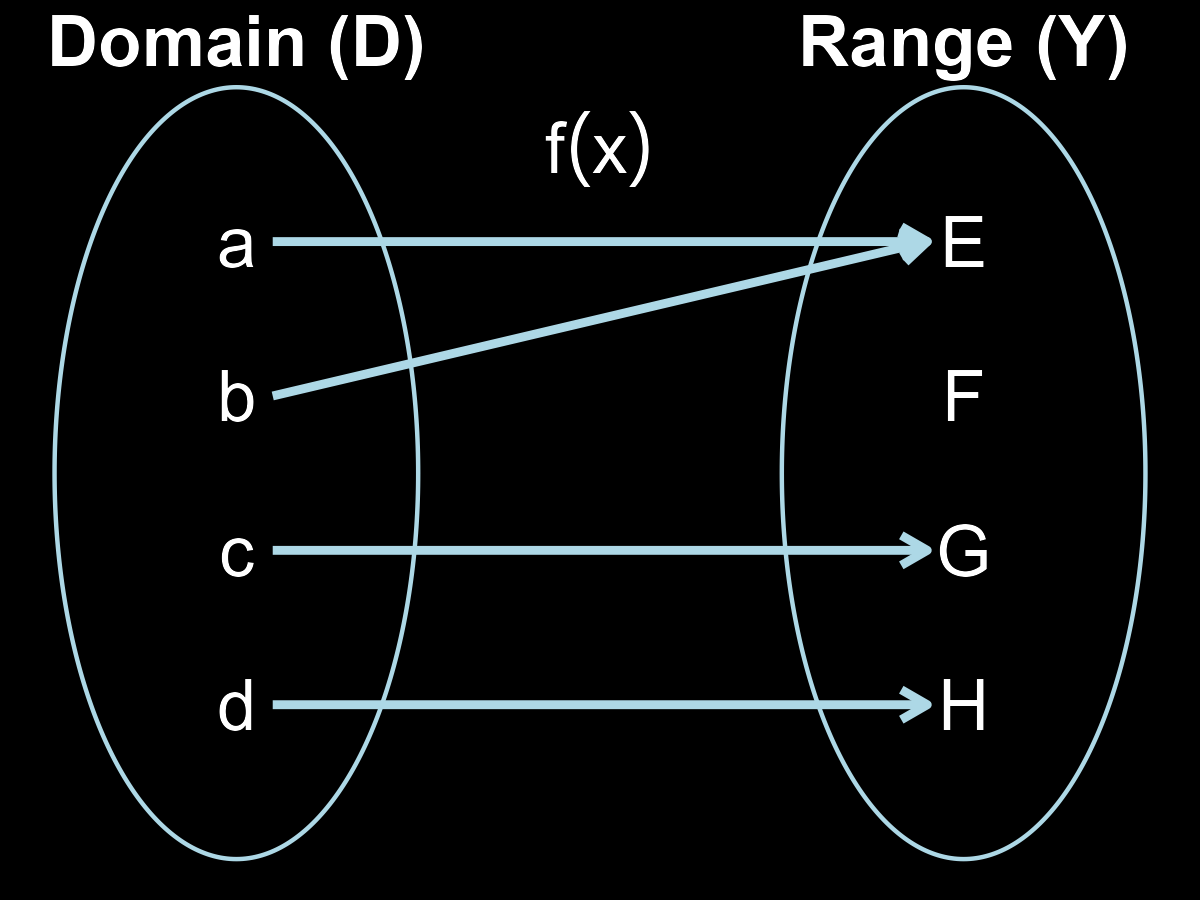
Here, \(x\) can take on four specific values: \(a\), \(b\), \(c\), and \(d\). When we input \(a\) into the function, we get \(f(a) = E\), meaning that the function maps \(a\) to \(E\). Similarly, \(f(b) = E\), so both \(a\) and \(b\) are mapped to the same value \(E\).

Likewise:

• \(f(c) = G\)
• \(f(d) = H\)

This example illustrates the rule of functions: each element in the domain must be assigned to one and only one element in the range. That means no element in the domain is left unmapped.

However, not every element in the range needs to be used. In this case, the value \(F\) in the range has no domain element mapping to it, and that is acceptable in the definition of a function.