Understanding Number Systems in Mathematics

When we study mathematics, we encounter various number systems. Instead of going into rigorous definitions, let’s just briefly explore them.

Natural Numbers

Natural numbers ($\mathbb{N}$) are the numbers we use for counting and ordering. They start from 1 and go on infinitely:

$$
\mathbb{N} = \{1, 2, 3, 4, 5, …\}
$$

Some definitions also include 0 in natural numbers, depending on the context.

Whole Numbers

Whole numbers are like natural numbers but they include 0:

$$
ℕ₀ =\{0, 1, 2, 3, 4, …\}
$$

Integers

Integers ($\mathbb{Z}$) expand whole numbers by including negative numbers:

$$
\mathbb{Z} = \{…, -3, -2, -1, 0, 1, 2, 3, …\}
$$

Integers are useful for expressing losses, debts, or temperatures below zero.

Rational Numbers

Rational numbers ($\mathbb{Q}$) are numbers that can be expressed as a fraction of two integers, where the denominator is not zero:

$$
\mathbb{Q} = \{ \frac{p}{q} : p, q \in \mathbb{Z}, q \neq 0 \}
$$

Examples: 1/2, 5/3, and 7 (since 7 = 7/1).

Rational numbers can also be written as terminating or repeating decimals (e.g., 0.75, 0.333…).

Irrational Numbers

Irrational numbers cannot be expressed as fractions of two integers. Their decimal expansions are non-terminating and non-repeating. Examples:

$\pi = 3.14159…$
$\sqrt{2} = 1.41421…$

Real Numbers

The set of real numbers ($\mathbb{R}$) combines both rational and irrational numbers. Essentially, any number that can be placed on the number line is a real number:

$$
\mathbb{R} = \mathbb{Q} \cup \{\text{Irrational Numbers}\}
$$

Complex Numbers

Some equations, like $x^2 + 1 = 0$, have no solution in the real numbers. To address this, mathematicians introduced complex numbers ($\mathbb{C}$):

$$
\mathbb{C} = {a + bi : a, b \in \mathbb{R}, i^2 = -1}
$$

Here, $a$ is the real part, and $bi$ is the imaginary part.

Examples: $2 + 3i$, $-5i$, $4$ (since $4 + 0i$).

Well, the +, −, ×, and ÷ operations for complex numbers are defined differently from those of real numbers that we use in everyday life, so let’s explore some basic operations along with other concepts frequently used in mathematics.

Addition/Subtraction:

$$
(a+bi) \pm (c+di) = (a \pm c) + (b \pm d)i
$$

Multiplication:

$$
(a+bi)(c+di) = (ac – bd) + (ad + bc)i
$$

Conjugate: If $z = a + bi$, then $\bar{z} = a – bi$.
Division (multiply both numerator and denominator by the conjugate of the denominator ($c – di$)):

$$
\frac{a+bi}{c+di} \;=\; \frac{(a+bi)(c-di)}{(c+di)(c-di)} \;=\; \frac{(a+bi)(c-di)}{c^2+d^2}
$$

Modulus (magnitude):

$$
|z| = \sqrt{a^2 + b^2}
$$

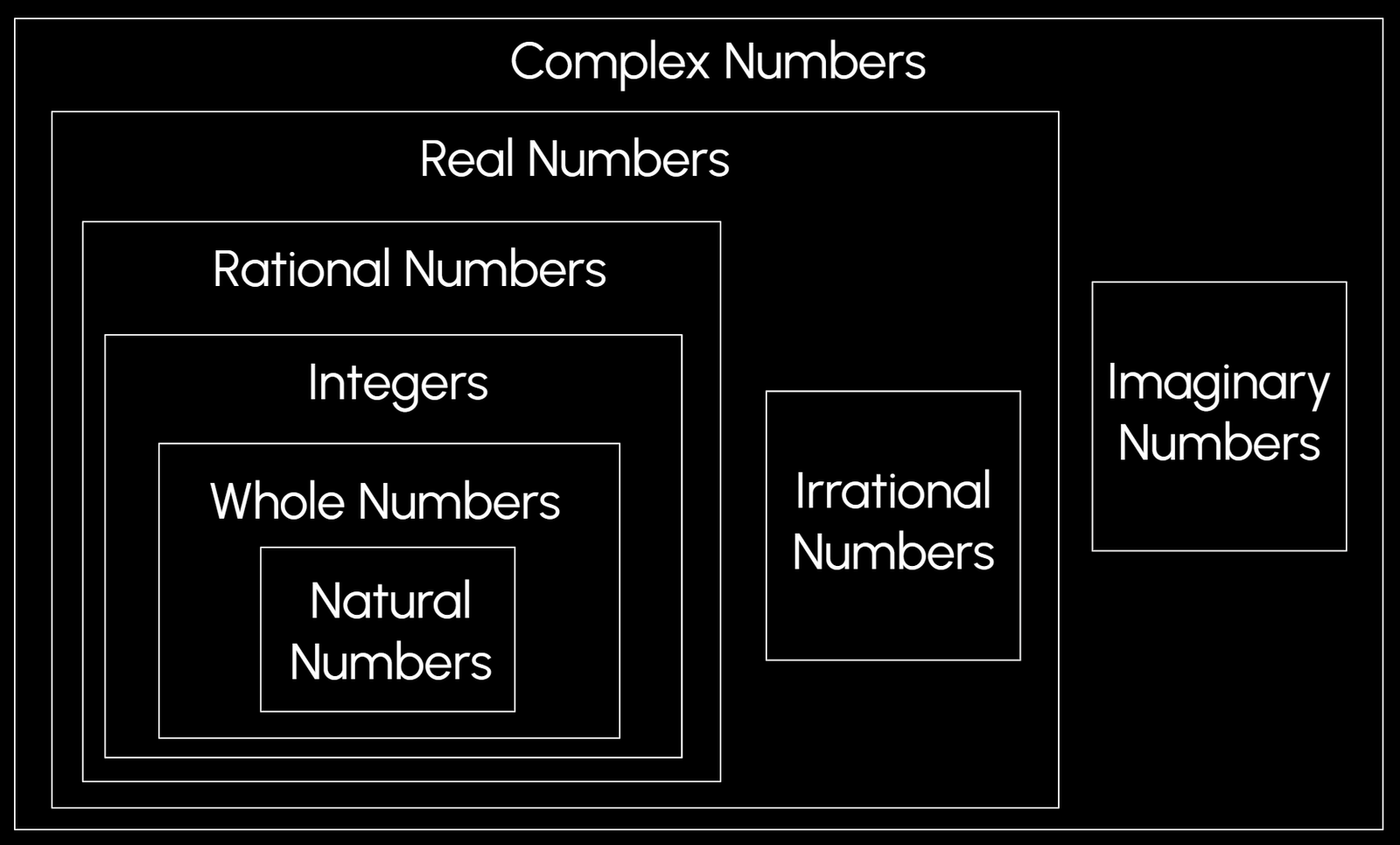
A Hierarchy of Numbers

The number systems are nested inside one another:

Hierarchy diagram of number systems showing natural numbers, whole numbers, integers, rational numbers, irrational numbers, real numbers, complex numbers, and imaginary numbers.

Why Are These Number Systems Important?

Each expansion of the number system was developed to solve problems that earlier systems couldn’t handle:

Natural numbers: Counting objects.
Whole numbers: Including zero for nothingness.
Integers: Representing losses and opposites.
Rational numbers: Expressing parts of a whole.
Irrational numbers: Measuring quantities like square roots and circles.
Real numbers: Continuous measurement on the number line.
Complex numbers: Solutions to advanced equations in engineering, physics, and beyond.

Final Thoughts

Understanding number systems is fundamental for deeper studies in mathematics. Each system builds on the previous one, extending our ability to describe the world and solve increasingly complex problems. From counting apples to solving quantum equations, the journey through number systems reflects the power of human curiosity and logic.